D3. Elementary algebra : simultaneous linear equations.
Equations like y=2x+5 or y-4x=3 are called linear
equations. They each contain two unknown quantities, x and y, and could be
plotted to produce straight line graphs.
Two of these lines might cross - or a have a point of intersection. We
can use a graph or algebra to find the coordinates of this point of
intersection. |
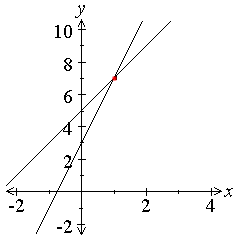 |
If you want to find out more about using graphs to solve
simultaneous equations, then go to graphical
method.
The following shows how to solve simultaneous linear
equations by algebra using the method of eliminating one of the unknown
quantites x or y.
Example: solve y=2x+5 and y-4x=3
| Step 1: |
Number the equations |
y=2x+5 (1)
y-4x=3 (2) |
| Step 2: |
Rearrange the equations so they are both written in a
similar way: |
y=2x+5 (1)
y=4x+3 (2) |
| Step 3: |
Subtract (1) from (2) to eliminate y |
0=2x-2 |
| Step 4: |
Solve this equation: |
x=1 |
| Step 5: |
Substitute this value into one of the original equations
to find y: |
y=2(1)+5 = 7 |
| Step 6: |
Check the two values do fit in both original
equations |
|
Example: solve 2x+3y=5 and 3x=4y-1
| Step 1: |
Number the equations |
2x+3y=5 (1)
3x=4y-1 (2) |
| Step 2: |
Rearrange the equations so they are both written in a
similar way: |
2x+3y=5 (1)
3x-4y=-1 (2) |
| Step 3: |
Multiply (1) by 3 and multiply (2) by 2
(Why?) |
6x+9y=15 (1)
6x-8y=-2 (2) |
| Step 4: |
Subtract (2) from (1) to eliminate x |
17y=17 |
| Step 5: |
Solve this equation: |
y=1 |
| Step 6: |
Substitute this value into one of the original equations
to find x: |
3x=4(1)-1
x=1 |
| Step 7: |
Check the two values do fit in both original
equations |
|
Why? This step needs to be understood
clearly. The purpose in this case is to have the same quantity of x in both
equations so that x can be eliminated.
Here is another way of displaying the process of solving two
simultaneous equations. You can alter the two equations between the red lines.
|

![[Advert]](../../images/ad/content.gif)

![[Advert]](../../images/ad/content.gif)
